Alpha Beta Pruning is an optimization technique of the Minimax algorithm. This algorithm solves the limitation of exponential time and space complexity in the case of the Minimax algorithm by pruning redundant branches of a game tree using its parameters Alpha(α) and Beta(β).
Parameters of the Alpha Beta Pruning Algorithm
-
Alpha(α): The best choice(highest utility/value) found till the current state on the path traversed by the maximizer.
-
Beta(β): The best choice(lowest utility/value) found till the current state on the path traversed by the minimizer.
Working on Alpha Beta Pruning Algorithm
To illustrate the working of Alpha Beta Pruning in AI, we use an example game tree shown in Figure-1. The numbers shown in terminal nodes represent their respective utilities.
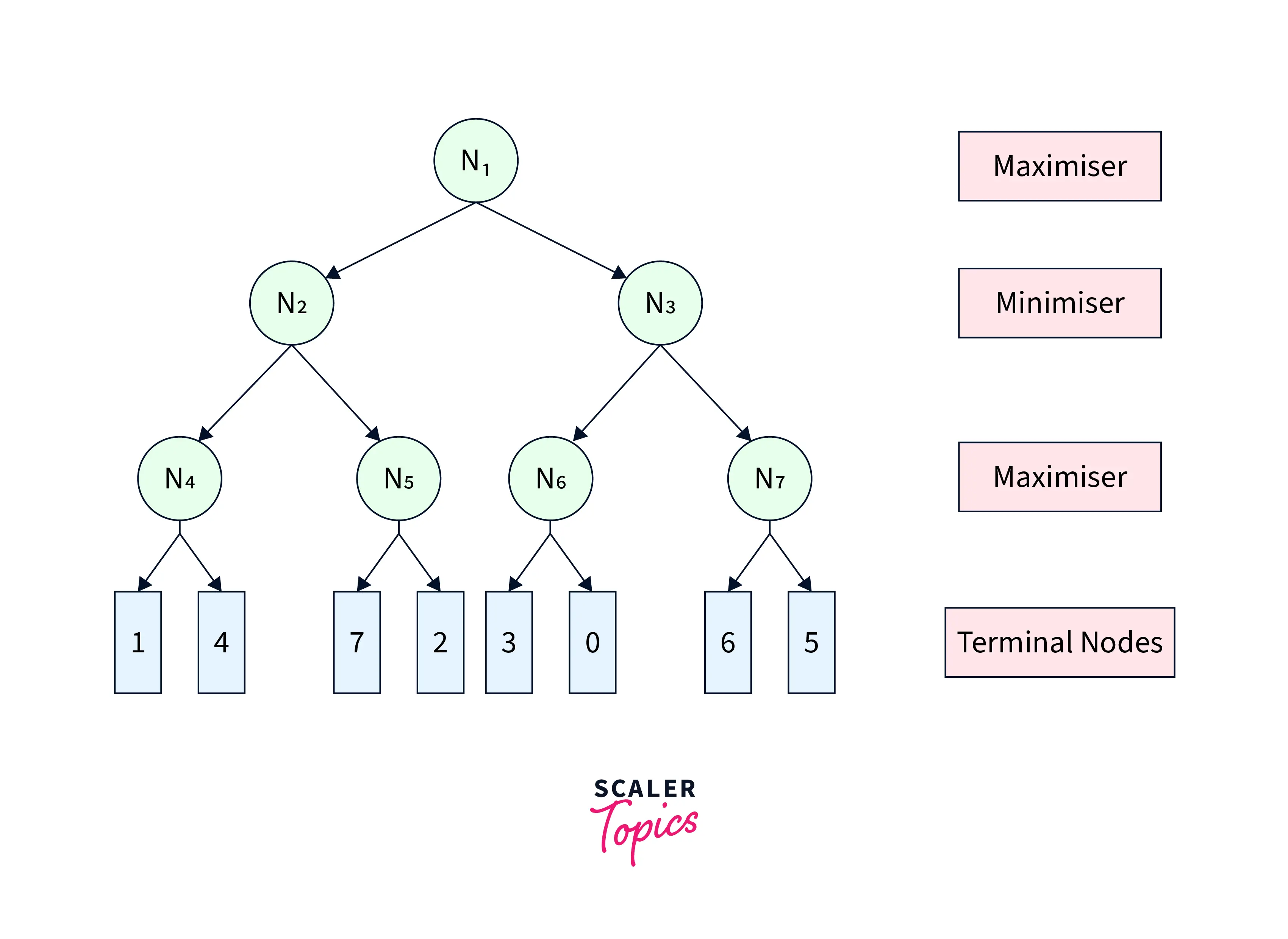 |
|---|
| Figure-1 |
The Minimax algorithm would have traversed the complete game tree leading to the game tree shown in Figure-2.
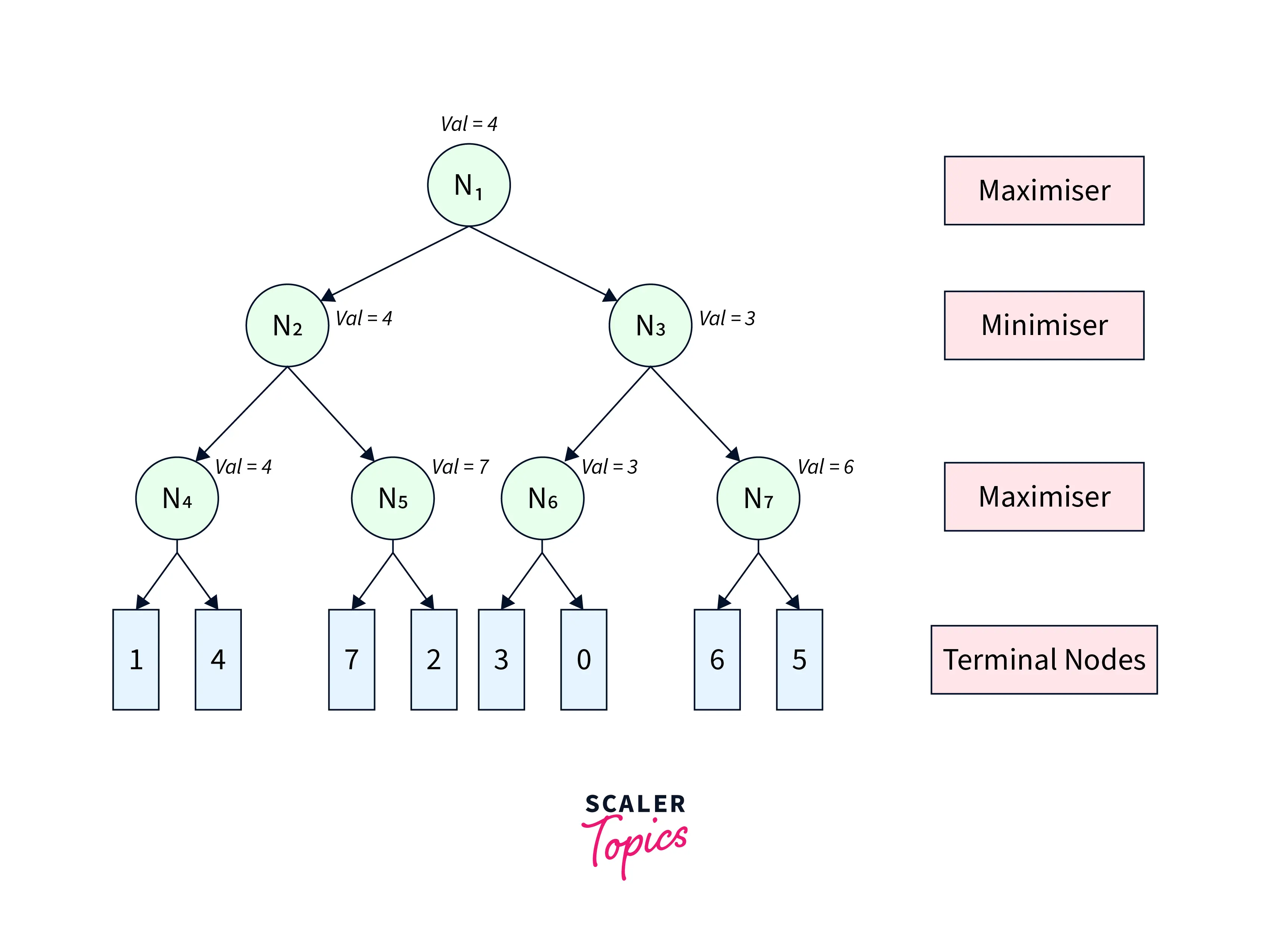 |
|---|
| Figure-2 |
Alpha Beta Pruning algorithm restricts the agent from visiting redundant sub-trees leading to faster average search time complexity. To visualize its working, we refer to the same game tree in Figure-1. We start from node N1 with α=− and β=∞β=∞. From N1, we move to its child node N2 with the same αα and ββ. Similarly, we move from N2 to its child N4, as shown in Figure-3.
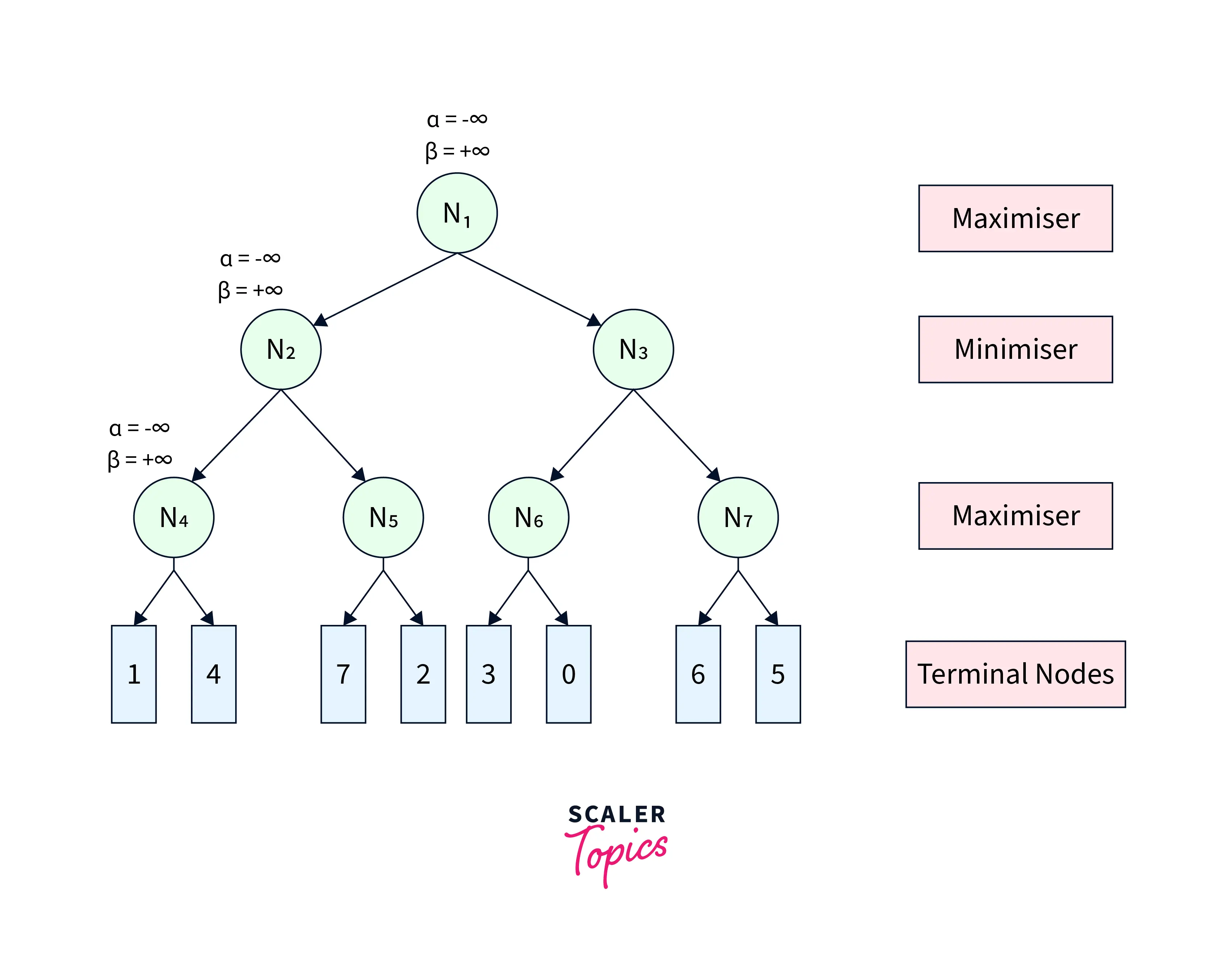 |
|---|
| Figure-3 |
From N4, we move to its first terminal child and get back its utility as 11. Since N4 is a maximiser, we update α=max(−∞,1)=1α=max(−∞,1)=1. The pruning condition α≥βα≥β remains unsatisfied. Therefore, we move to the second terminal child of N4 and get its utility as 44. Further, we update α=max(1,4)=4α=max(1,4)=4. After this step, we get the node value of N4 as max(1,4)=4max(1,4)=4 and return it to its parent N2. Since N2 is a minimiser, it updates β=min(+∞,4)=4β=min(+∞,4)=4. The game tree after this step is shown in Figure-4.
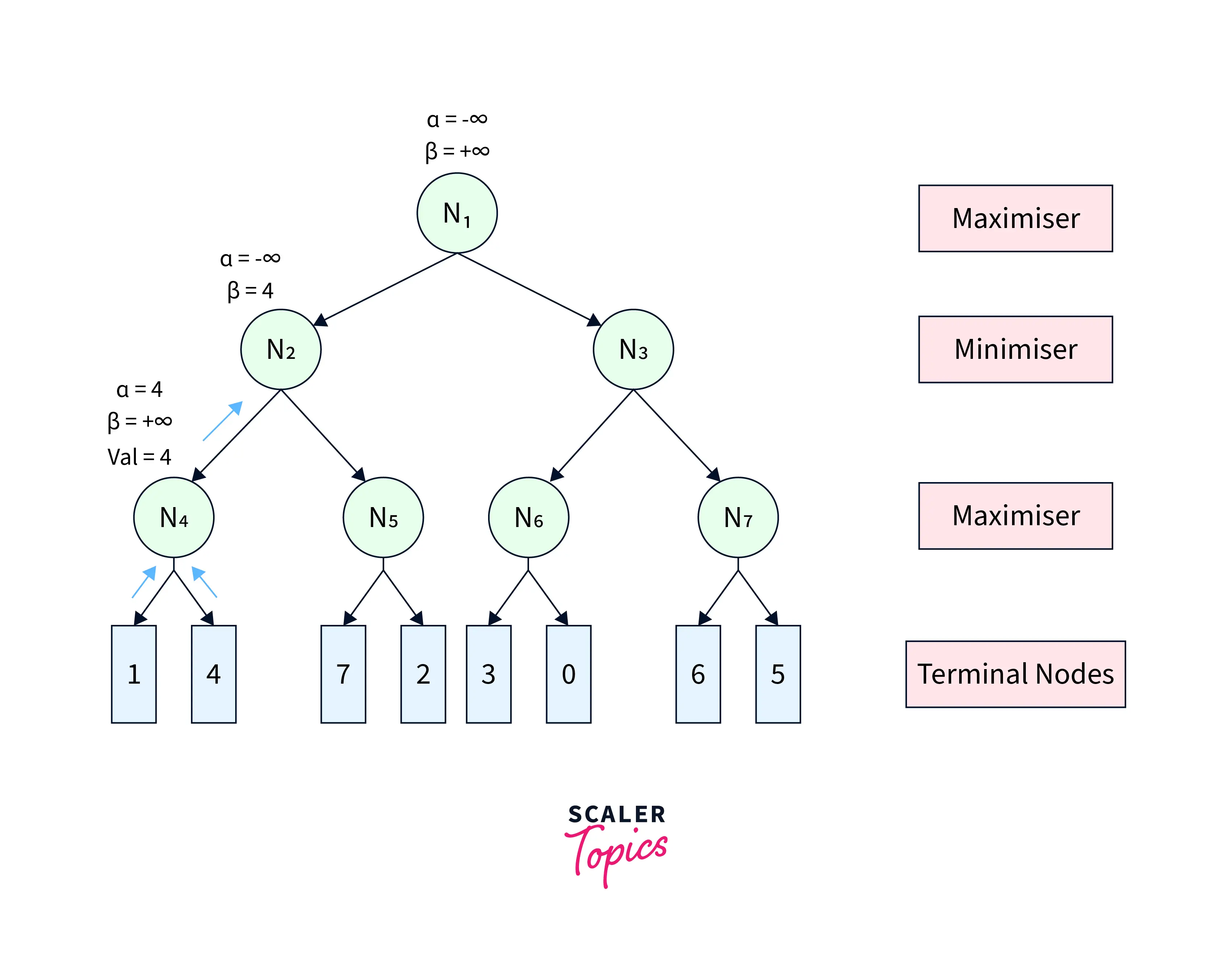 |
|---|
| Figure-4 |
At N2, the pruning condition α≥βα≥β is still unsatisfied. Therefore, we visit its next child node N5 with α=−∞α=−∞ and β=4β=4. At N5, we get the utility of its first terminal child as 77. Since N5 is a maximiser, we update α=max(−∞,7)=7α=max(−∞,7)=7. Now, the pruning condition gets satisfied (7≥4)(7≥4), leading to the pruning of the other child node. After that, the node utility of N5=7N5=7 is further sent back to the parent node N2. N2 updates β=min(4,7)=4β=min(4,7)=4. Further, the node value of N2=min(4,7)=4N2=min(4,7)=4 is returned to its parent N1. At N1, we update α=max(−∞,4)=4α=max(−∞,4)=4. After this step, the game tree looks like Figure-5.
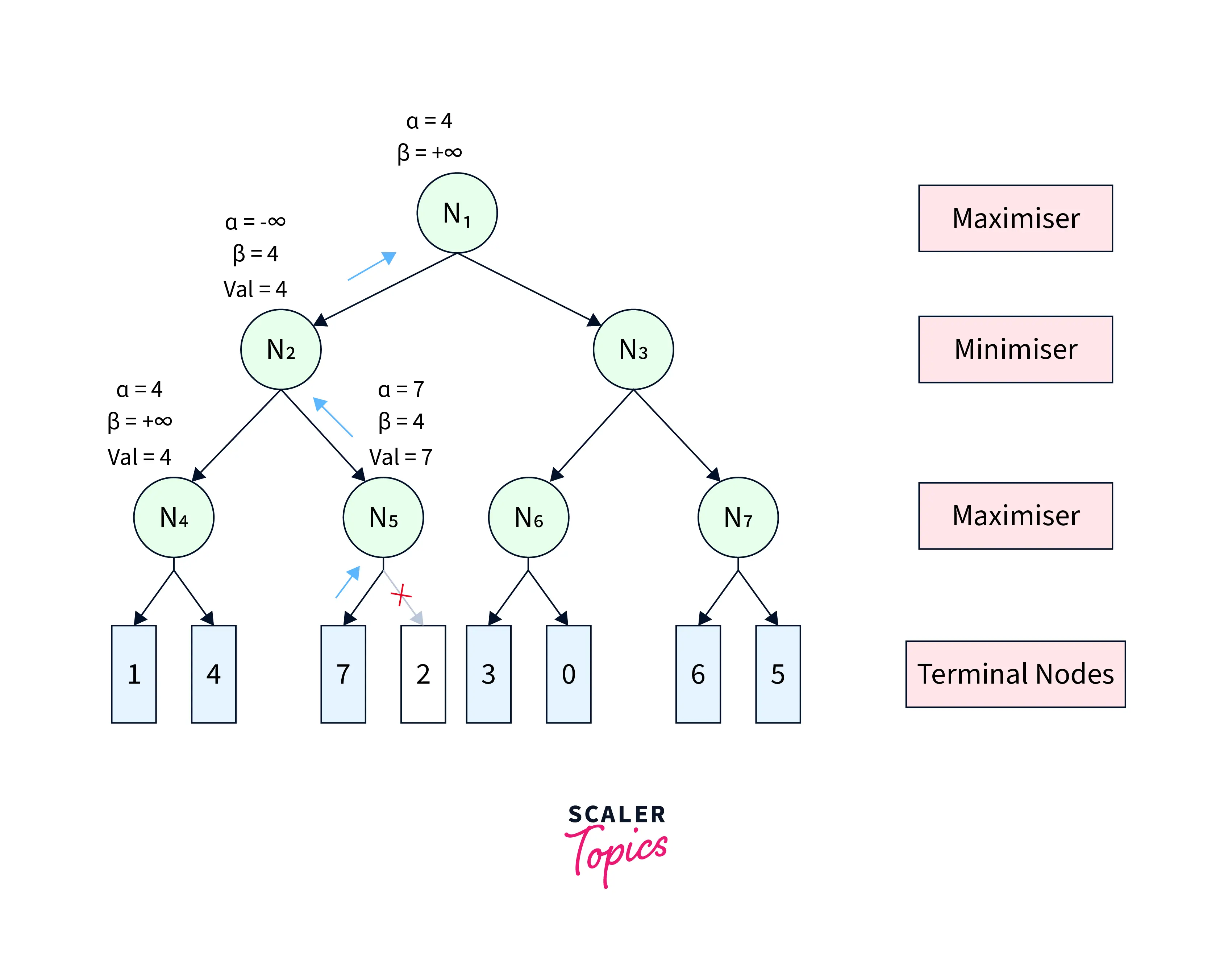 |
|---|
| Figure-5 |
The pruning condition is still unsatisfactory at N1. Therefore, we continue towards the next child N3, with the same values of αα and ββ. Similarly, we propagate from N3 to its first child N6. At N6, we get back the utility of its first terminal child as 33 and update α=max(4,3)=4α=max(4,3)=4. Since the pruning condition is still unsatisfied, we get the utility of the second terminal child as 00 and update α=max(4,0)=4α=max(4,0)=4. After this, the node value of N6=max(3,0)=3N6=max(3,0)=3, is returned to the parent N3. Since N3 is a minimiser, we update β=min(+∞,3)=3β=min(+∞,3)=3. Now, the pruning condition gets satisfied (4≥3)(4≥3). Therefore, the other child sub-tree(rooted at N7) of N3 is pruned, and the node value of N3 becomes 33, which is returned to parent N1. At N1, we again update α=max(4,3)=4α=max(4,3)=4 and the final utility of N1 becomes 44. All these steps are shown in Figure-6.
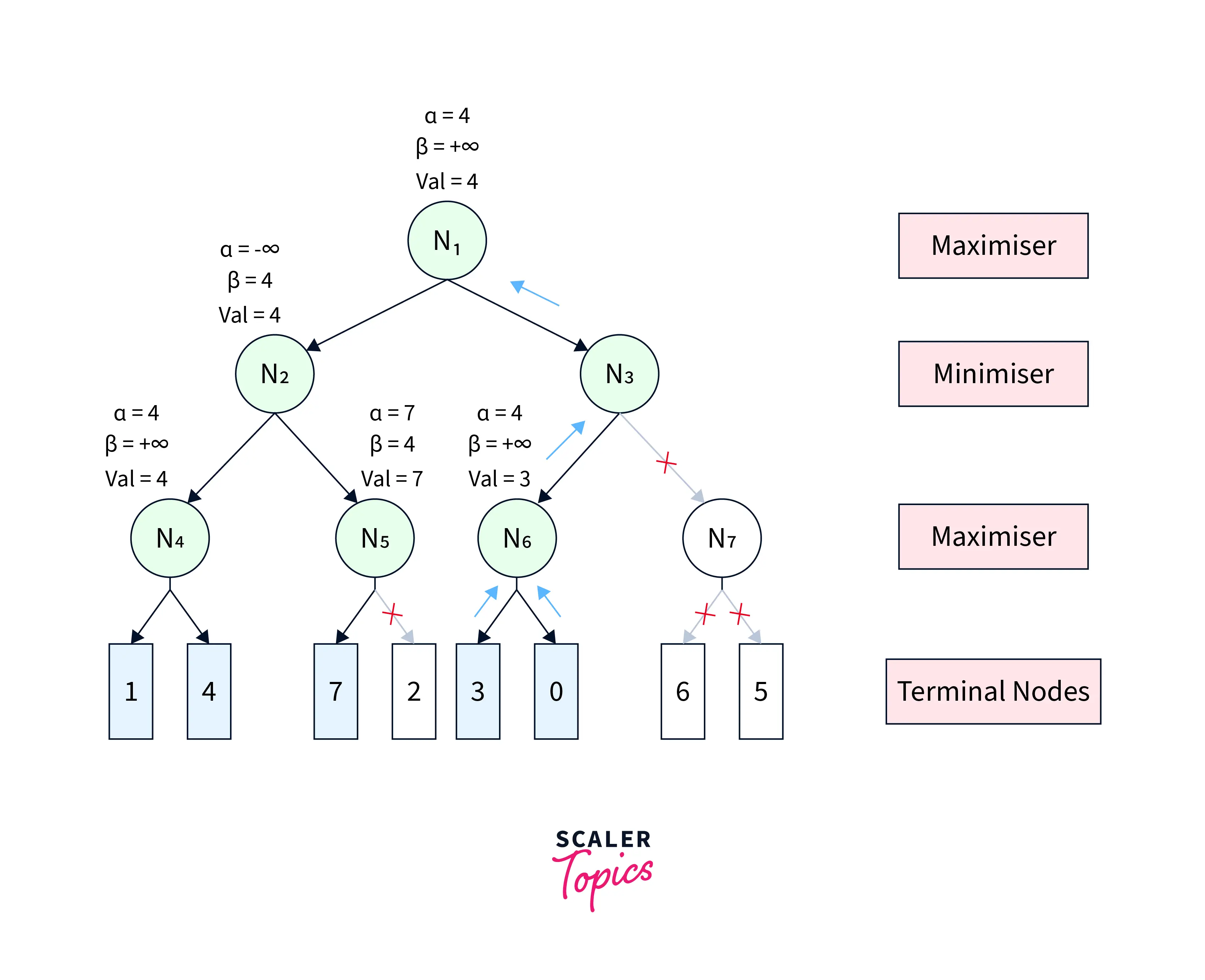 |
|---|
| Figure-6 |
Figure-6 depicts the final game tree of the Alpha Beta Pruning algorithm. As evident from the figure, Alpha Beta Pruning in AI yields the same result as the Minimax algorithm by visiting fewer states.
Move Ordering in Alpha Beta pruning in AI
The performance of the Alpha Beta Pruning algorithm is highly dependent on the order in which the nodes are traversed. For instance,
Case-1(Worst Performance): If the best sequence of actions is on the right of the game tree, then there will be no pruning, and all the nodes will be traversed, leading to even worse performance than the Minimax algorithm because of the overhead of computing αα and β. Case-2(Best Performance): If the best sequence of actions is on the left of the game tree, there will be a lot of pruning, and only about half of the nodes will be traversed to get the optimal result.